Patching SpEL for Better Compilation Performance

The Spring Expression Language (SpEL) is an expressive language that is typically used for computing simple expressions. To provide better performance in latency-sensitives cases, SpEL can compile expressions by generating bytecode instead of evaluating the expressions in interpreted mode. This can result in a drastic performance boost, with reported speedups of 25x, 36x and even 58x in one case.¹ This makes SpEL a candidate for hot paths, such as logging and high-volume event processing.

There are however a few caveats to this, one of which makes it impossible to know whether an expression containing things like boolean operators is compilable, unfortunately making the SpEL compiler unreliable for critical scenarios, such as high-volume data processing or logging filters.

In this article, we will discuss this limitation, and see how we can address it by patching the SpEL runtime. In the process, we will learn about the internals of SpEL. We will then discuss an application of this in a Logback logging filter. Finally, we will see a potential solution to the root cause of this issue.

The SpEL compiler

By default, SpEL compilation is disabled, and expressions run in interpreted mode. We can enable compilation either for a specific SpelExpression by setting CompilerMode.IMMEDIATE or CompilerMode.MIXED on the parser’s configuration, or globally, by setting the spring.expression.compiler.mode property to immediate or mixed (docs). Under immediate, an expression will run in interpreted mode the first time around, and will then run in compiled mode from then on, given that the expression is compilable (more on that later). Under mixed, a given expression will run in interpreted mode, and after a number of iterations (currently 100), it will be compiled and start running in compiled mode. mixed therefore acts as a sort of JIT compiler, optimizing only the expressions that run often.

The immediate and mixed modes also have different error handling characteristics. If a compiled expression fails under immediate, the exception will be propagated to the caller, and the next invocation will still use the compiled expression. Under mixed, if a compiled expression fails, the exception is swallowed, the compiled classes are discarded, and the expression reverts to interpreted, until it becomes eligible for compilation again (after another 100 invocations).

Only a subset of SpEL is compilable. For instance, expressions using assignment, bean references, or collection projections are not compilable. But the most important limitation, in my opinion, is due to the way the compiler gets its typing information:

Due to the lack of typing around expressions, the compiler uses information gathered during the interpreted evaluations of an expression when performing compilation. For example, it does not know the type of a property reference purely from the expression, but during the first interpreted evaluation, it finds out what it is.

In other words, some SpEL Abstract Syntax Tree (AST) nodes are only compilable if they have been previously executed in interpreted mode, or if all of their children nodes have been evaluated. This is a problem for the and and or boolean operators, since they don’t always evaluate both of their operands. Take the following expressions:

true and true   // left and right side are evaluated
true and false  // left and right side are evaluated
false and false // only left side
false and true  // only left side

If we write the expression false and true using boolean literals, SpEL will still be able to compile it, because it knows the types of boolean literals from the get go. But if we add an indirection to the mix, and the operands are method calls or property accesses, SpEL can no longer know the type of the operands before evaluating them, and therefore it cannot compile the expression, even if the left and right operands are themselves compilable expressions. The following test reproduces this issue:

@Test
void unCompilableExpression() {
  // declare and parse an expression
  Expression expression = new SpelExpressionParser().parseExpression("left and right");

  // set the values of "left" and "right" on the evaluation context
  SimpleEvaluationContext context = SimpleEvaluationContext.forReadOnlyDataBinding()
    .withRootObject(new ExpressionRoot(false, true))
    .build();

  // SpelCompiler.compile() tries to compile the expression,
  // returning true if it succeeded, and false otherwise.
  // If true, further evaluations of the `SpelExpression` will
  // run in compiled mode.
  assertThat(SpelCompiler.compile(expression))
    .isFalse();

  // evaluate the expression
  assertThat(expression.getValue(context))
    .isEqualTo(false);

  // check that the expression is compilable;
  // this fails because the right operand has not been evaluated yet
  assertThat(SpelCompiler.compile(expression))
    .isTrue();
}

public record ExpressionRoot(boolean left, boolean right) {
}

If we run this test again with a new ExpressionRoot(true, true) evaluation context, we’ll see that this time, the expression does compile after we evaluate it. The difference depends only on short-circuiting behaviour of the and operator. This short-circuiting behaviour is not unique to boolean operators: ternary operators, and even the “null-safe index operator” (.?) are also affected.

This is problematic, because it means that as soon as you have any boolean operators, ternary operators, or null-safe operators (?.) in a SpEL expression, its compilability is non-deterministic. Consider this expression:

T(java.util.concurrent.ThreadLocalRandom).current().nextBoolean() && right

Is it compilable? Depends on what nextBoolean() evaluated to in the “training runs”. But what if we need the expression to compile, because we can’t afford to pay the performance cost of interpreted mode? Well, we might just have to get creative…

The Solution

A possible solution to this is to ensure that there are no short-circuiting operators in the expressions. Unfortunarely, this would mean significantly restricting the language.

Actually, there’s a solution to this that works for boolean and ternary operators. It doesn’t work with ?., but if we can cover boolean and ternary, that’s already a good improvement. The solution we’ll discuss is to patch the boolean and ternary operators so that they don’t short-circuit, at least not the first time around, so that the interpreter can build up the necessary type information for the compilation to kick in. This way, we can guarantee that an expression is compilable during application startup.

Sounds like a plan? Let’s get started.

Hacking SpEL

Before we get our hands dirty, a quick word about the SpEL interpreter. It’s a tree-walk interpreter, meaning it traverses an Abstract Syntax Tree (AST) and evaluates the nodes as it goes.² SpEL nodes implement the SpelNode interface and know how to both interpret and compile themselves. Here is an overview of the SpelNode interface:

public interface SpelNode {
  // ...
  @Nullable
  Object getValue(ExpressionState expressionState) throws EvaluationException;

  int getChildCount();

  SpelNode getChild(int index);

  default void generateCode(MethodVisitor methodVisitor, CodeFlow codeFlow) {
    // throw exception if not implemented
  }
  // ...
}

This interface is directly implemented by a single abstract class, SpelNodeImpl, that in turn is extended by a grand total of 21 classes: OpAnd and OpOr for the and and or operators, Ternary for ternary, but also ConstructorReference, Assign, Elvis (the Elvis operator), MethodReference, and BeanReference. The AST root is therefore a SpelNode and we can traverse the tree by accessing each node’s children using their getChild(int) method. We can get this AST by calling getAst() on a parsed SpEL expression.

Knowing this, here is how we can ensure that SpEL expressions are not non-compilable because of short-circuiting operators. We’ll intercept the SpelExpression coming from a SpelExpressionParser, inspect its AST, and modify it by swapping out the OpAnd, OpOr, and Ternary nodes for custom nodes that will run the first evaluation without short-circuiting.³

We’ll do this in three parts. First, we’ll write a SpelExpressionParser that we can use to intercept the AST. Second, we’ll write custom AST nodes to implement our logic. And third, we’ll modify the AST to use our custom nodes.

Step 1: Writing a custom parser (kind of)

When I think “intercepting a return value”, the design pattern that springs to mind is Decorator. Just implement an interface or extend a class, and accept a class to delegate invocations to. So we’ll kind of write a parser, in the sense that we’ll be extending SpelExpressionParser, but we will delegate all the heavy lifting to the regular SpelExpressionParser:

@RequiredArgsConstructor
public class CustomSpelExpressionParser extends SpelExpressionParser {

  private final SpelParserConfiguration configuration =
    new SpelParserConfiguration(SpelCompilerMode.IMMEDIATE, null);
  private final SpelExpressionParser delegate = new SpelExpressionParser(configuration);

  @Override
  public Expression parseExpression(String expressionString,
                                    @Nullable ParserContext context) throws ParseException {

    SpelExpression expression =
      (SpelExpression) delegate.parseExpression(expressionString, context);

    // yay!
    SpelNode ast = expression.getAST();

    return expression;
  }
}

Now that we just wrote a complete parser in 5 minutes 🤓, let’s see how we can modify the AST nodes concerning us.

Step 2: Custom AST nodes

What we want is to “patch” boolean and ternary operators so that they won’t short-circuit the first time around, so that the interpreter can build up the necessary type information for the compiler. As we saw earlier, all SpEL AST nodes have one method, getValueInternal, that they implement in order to provide their evaluation behaviour. For OpAnd, that’s just evaluating the two expressions at the left and at the right of the operator, while obeying the short-circuiting contract:

public class OpAnd extends Operator {
  // ...
  public TypedValue getValueInternal(ExpressionState state) throws EvaluationException {
    if (!getBooleanValue(state, getLeftOperand())) {
      return BooleanTypedValue.FALSE;
    }
    return BooleanTypedValue.forValue(getBooleanValue(state, getRightOperand()));
  }
  // ...
}

OpOr and Ternary do pretty much the same thing, so from now on, we’ll only worry about OpAnd. Already, we can see that the boolean ASTs are nothing special. Actually, they are a bit special, since they know how to generate bytecode equivalent to their getValueInternal method to compile themselves, but we don’t have to worry about that.⁴ The good thing is, as long as we force the expressions to run in compiled mode right from the second evaluation by setting CompilerMode.IMMEDIATE on the expression, they will use the default behaviour, and we don’t have any work to do!

class NonShortCircuitingWhenInterpretedAnd extends OpAnd {

  public NonShortCircuitingWhenInterpretedAnd(int startPos, int endPos,
                                              SpelNodeImpl... operands) {
    super(startPos, endPos, operands);
  }

  @Override
  public TypedValue getValueInternal(ExpressionState state) throws EvaluationException {
    Boolean left = (Boolean) getLeftOperand().getValue(state);
    Boolean right = (Boolean) getRightOperand().getValue(state);

    return BooleanTypedValue.forValue(left && right);
  }
}

I’m omitting some null-checking and error reporting from the snippet above to keep this article simple, but that’s really all there is to it.

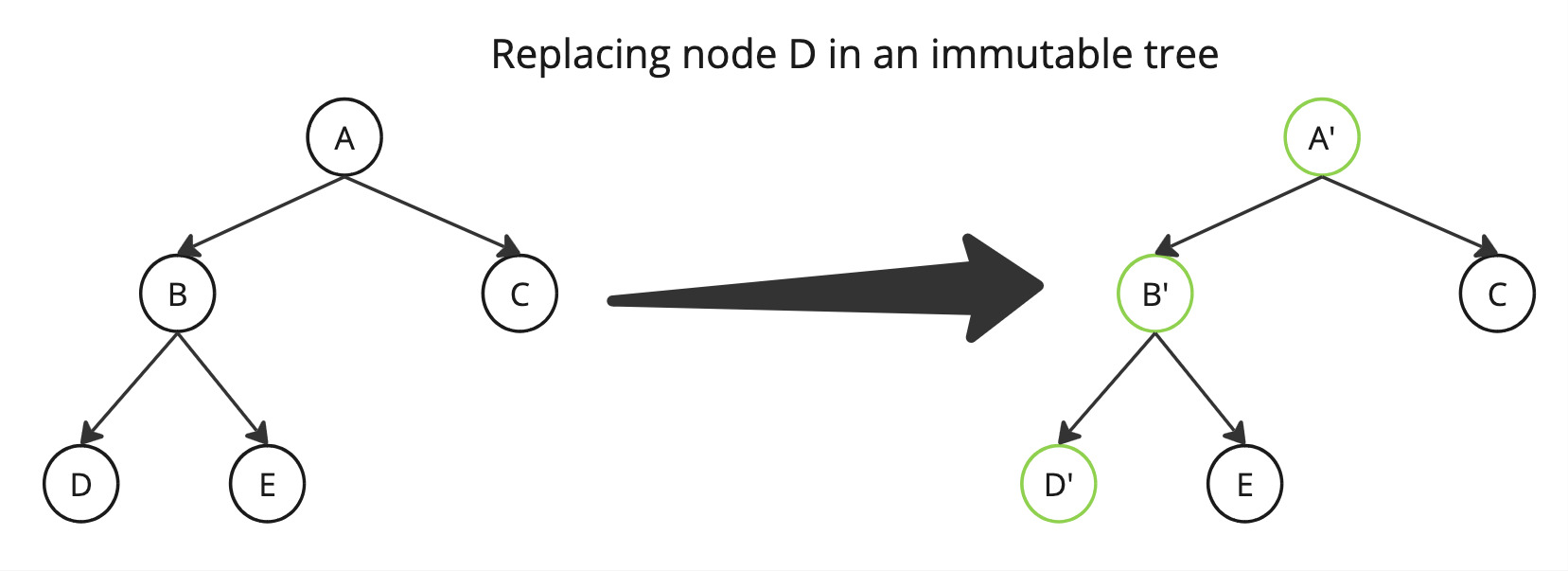
Now, let’s see how we can modify the AST to replace OpAnd, OpOr, and Ternary with our custom nodes. The AST is an immutable data structure and is a tree, so we’ll use a standard post-order traversal. The AST nodes are immutable, so to swap out a node, we actually have to copy everything up to from that node. It helps to visualize this problem. In the image below, if we want to replace node D, we also have to “tell” node B that its left child is now D′, and repeat the process for node A. And since nodes are immutable, we need to replace them with a copy that contains the updated children.

One limitation of doing this with SpEL nodes is that some node types, like Assign, which represents the SpEL assignment operator, don’t expose the necessary methods to copy the nodes. So to keep this article simple, and also because it is sufficient for many cases, we will only swap out OpAnd, OpOr, and Ternary nodes that are either top-level or direct children of other OpAnd, OpOr or Ternary nodes. This means that we will be able to handle this expression:

#exception instanceof T(IllegalArgumentException) 
and 
#exception.message matches '[ERROR].*' 
or 
#myVar > 5 

but not this one:

#logger.log(true && false)

because the OpAnd is a child of the node representing the #logger.log operation. This limitation is not significant, since boolean expressions in SpEL are usually used directly.

Step 3: modifying the AST

And with this, we can write the rest of our parser:

@Override
public Expression parseExpression(String expressionString,
                                  @Nullable ParserContext context)
  throws ParseException {
  SpelExpression expression =
    (SpelExpression) delegate.parseExpression(expressionString, context);

  SpelNode ast = expression.getAST();

  return new SpelExpression(
    expressionString,
    transformAst((SpelNodeImpl) ast),
    configuration
  );
}

public SpelNodeImpl transformAst(SpelNodeImpl root) {
  return switch (root) {
    case OpAnd opAnd -> new NonShortCircuitingWhenInterpretedAnd(
      opAnd.getStartPosition(),
      opAnd.getEndPosition(),
      // recursive case
      transformChildren(getChildren(opAnd)));
    case OpOr opOr -> new NonShortCircuitingWhenInterpretedOr(
      opOr.getStartPosition(),
      opOr.getEndPosition(),
      // recursive case
      transformChildren(getChildren(opOr)));
    case Ternary ternary -> new NonShortCircuitingWhenInterpretedTernary(
      ternary.getStartPosition(),
      ternary.getEndPosition(),
      // recursive case
      transformChildren(getChildren(ternary)));
    // base case
    default -> root;
  };
}

private SpelNodeImpl[] transformChildren(SpelNodeImpl... children) {
  return Arrays.stream(children)
    .map(this::transformAst)
    .toArray(SpelNodeImpl[]::new);
}

private SpelNodeImpl[] getChildren(SpelNodeImpl root) {
  SpelNodeImpl[] children = new SpelNodeImpl[root.getChildCount()];
  for (int i = 0; i < root.getChildCount(); i++) {
    children[i] = (SpelNodeImpl) root.getChild(i);
  }
  return children;
}

// implementations of the AST nodes...

Now if we use this custom parser to run the test at the beginning of this article, we’ll see that it now passes, and the expression compiles just fine!

Applying this to a Logback Filter

I first stumbled upon the problem of boolean operator compilability when writing a Logback TurboFilter. We wanted to be able to downgrade an ERROR log to INFO whenever it matched an arbitrary expression, so that our error logs wouldn’t get polluted by errors we knew could be ignored. I’ll be dedicating a separate article to this filter, because it came with interesting challenges, but here’s part of a logback.xml configuration demonstrating its usage:

<turboFilter class="com.example.filters.ExpressionBasedLevelConverterFilter">
  <!-- this is a SpEL expression -->
  <expression>
    level == ERROR
    and
    throwable instanceof T(java.lang.IllegalArgumentException)
    and
    throwable.message == 'something specific'
    and
    logger == 'com.example.application.MyService'
  </expression>
  <onMatch>com.example.filters.ConvertLevelToInfo</onMatch>
</turboFilter>

Upon initialization, the filter will:

1. parse its expression
2. evaluate it once using dummy objects to populate the expression variables (level, throwable, logger, and a few others), as a “training run” for the compiler
3. compile it

If the expression is not compilable, the filter will throw an exception to prevent running the interpreted expression on a critical code path (TurboFilters are called on every log request). After this point, the filter is ready to run the compiled expression without adding undue latency to the application. And since the first evaluation of the expression uses dummy arguments, it doesn’t matter that the operators don’t short-circuit!

Could we just fix the root cause?

This whole issue with compilability is because the compiler uses the invokevirtual bytecode instruction (or opcode), which requires the type of the receiver at compile time. For example, when the statement "abc".length() is compiled using javac, the compiled class will contain the hardcoded string java/lang/String.length ()I.

Java 7 added the invokedynamic opcode, aimed at supporting dynamically typed languages. This opcode does not require a receiver type, making it suitable for compiling expressions where types are unknown at compile time. I suspect that the decision to go with the regular invokevirtual instead of invokedynamic in the SpEL compiler may have been because Spring 4, the version when the compiler was written, only had Java 6 as a baseline version. But the baseline of Spring 6 is Java 17, so now the compiler could possibly be improved by using invokedynamic.

Expressions could then be compiled even before having been evaluated. This would the issue with compilability that we’ve been discussing. It also has implications for native images, since if the expressions can be compiled at build time, the interpreter-specific parts of SpEL don’t even have to be compiled into the image.

Conclusion

We started by discussing how SpEL’s compiler can lead to notable performance improvements. It does have some limitations, one of which causes the compilability of expressions containing certain operators to be non-deterministic. We remediated this by patching the AST nodes corresponding to the boolean and ternary operators. Finally, we introduced a concrete application of this by introducing a Logback filter based on SpEL expressions, and we discussed a potential solution to the compilability problem.

This pattern of modifying the AST of a SpEL expression could be reused for other purposes. For instance, it is possible to extend the SpEL language to add new control-flow operators. Since AST nodes contain their index in the expression string, we could support & and | operators in an expression by replacing & by && and | by || and making a note of their position before sending the expression to the parser, then walking the AST tree and swapping just these nodes for our custom ones. We could also add boolean operators that evaluate their operands concurrently and short-circuit as soon as possible, which would save valuable time when the operands are blocking calls (ex: two different http requests).

One last note. In the logback filter we introduced, the non-short-circuiting behaviour is only present in the initial “training” run, and it uses dummy arguments, not real application data. I suspect that there are other cases that can work with the same pattern. It is important however not to expose this non-short-circuiting behaviour where it might interfere with the application at runtime, since users could rely on short-circuiting, for example by using the common idiom a != null && a.b().

The code from this article can be found here.

Footnotes

1. An early benchmark from 2013 even achieved a 1500x speedup by compiling an expression (!). I do not know if these results still stand, though. ↩︎

2. If you want to know more about ASTs and interpreters but don’t feel like getting a master’s degree in compilers, Ruslan Spivak has a series of articles called “Let’s Build a Simple Interpreter”. Part 7 covers ASTs and tree-walk interpreters. If you still find yourself wanting more, I can’t recommend enough Robert Nystrom’s Crafting Interpreters. It’s 600 pages long, but it’s a pleasant read and is packed with insights on computer science and software in general. ↩︎

3. This idea of swapping out nodes in the AST is not new. A user named “fanthos” had basically the same idea to fix a now-resolved shortcoming of function invocations. ↩︎

4. If you are curious about how the AST nodes generate bytecode, take a look at OpAnd.generateCode(). ↩︎